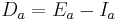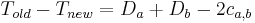Kernighan–Lin algorithm
- This article is about the heuristic algorithm for the graph partitioning problem. For a heuristic for the traveling salesperson problem, see Lin–Kernighan heuristic.
Kernighan–Lin is a O(n2 log n ) heuristic algorithm for solving the graph partitioning problem. The algorithm has important applications in the layout of digital circuits and components in VLSI.[1][2]
Description
Let 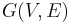 be a graph, and let
be a graph, and let  be the set of nodes and
be the set of nodes and  the set of edges. The algorithm attempts to find a partition of
the set of edges. The algorithm attempts to find a partition of  into two disjoint subsets
into two disjoint subsets  and
and  of equal size, such that the sum
of equal size, such that the sum  of the weights of the edges between nodes in
of the weights of the edges between nodes in  and
and  is minimized. Let
is minimized. Let 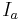 be the internal cost of a, that is, the sum of the costs of edges between a and other nodes in A, and let
be the internal cost of a, that is, the sum of the costs of edges between a and other nodes in A, and let 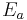 be the external cost of a, that is, the sum of the costs of edges between a and nodes in B. Furthermore, let
be the external cost of a, that is, the sum of the costs of edges between a and nodes in B. Furthermore, let
be the difference between the external and internal costs of a. If a and b are interchanged, then the reduction in cost is
where 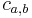 is the cost of the possible edge between a and b.
is the cost of the possible edge between a and b.
The algorithm attempts to find an optimal series of interchange operations between elements of  and
and  which maximizes
which maximizes 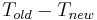 and then executes the operations, producing a partition of the graph to A and B.[1]
and then executes the operations, producing a partition of the graph to A and B.[1]
Pseudocode
See [2]
1 function Kernighan-Lin(G(V,E)): 2 determine a balanced initial partition of the nodes into sets A and B 3 do 4 A1 := A; B1 := B 5 compute D values for all a in A1 and b in B1 6 for (i := 1 to |V|/2) 7 find a[i] from A1 and b[i] from B1, such that g[i] = D[a[i]] + D[b[i]] - 2*c[a[i]][b[i]] is maximal 8 move a[i] to B1 and b[i] to A1 9 remove a[i] and b[i] from further consideration in this pass 10 update D values for the elements of A1 = A1 / a[i] and B1 = B1 / b[i] 11 end for 12 find k which maximizes g_max, the sum of g[1],...,g[k] 13 if (g_max > 0) then 14 Exchange a[1],a[2],...,a[k] with b[1],b[2],...,b[k] 15 until (g_max <= 0) 16 return G(V,E)
References
- ^ a b Kernighan, B. W.; Lin, Shen (1970). "An efficient heuristic procedure for partitioning graphs". Bell Systems Technical Journal 49: 291–307.
- ^ a b Ravikumār, Si. Pi; Ravikumar, C.P (1995). Parallel methods for VLSI layout design. Greenwood Publishing Group. pp. 73. ISBN 9780893918286. OCLC 2009-06-12. http://books.google.com/?id=VPXAxkTKxXIC.